| Les
coordonnées :
La
position des points d'une sphére est déterminée par
l'équation cartésienne suivante :
x² + y² + z² = r²
avec : r le rayon de la sphère et (x,y,z) les coordonnées
d'un point de la sphère dans l'espace virtuel. La partie gauche
de l'équation représente la norme au carré du vecteur
position (x,y,z), c'est à dire le carrée de distance entre
le centre de la sphère et l'endroit où nous nous situons.
La partie de droite est égale au carré du rayon de la sphère.
Pour être à la surface de celle-ci, il faut que ces deux
distances soit identiques. Cette équation n'est pas exploitable
sous cette forme, car pour l'instant elle nous permet plustot de tester
l'appartenance d'un point à une sphère que de nous données
ses coordonnées.
On
va donc ce placer en en coordonnées sphérique, où
l'on ne se repère plus grâce à x,y,z mais grâce
à Φ la latitude et θ la longitude :
r * sin(Φ) * cos(θ)
F(x,y,z)
= f(Φ,θ) = r * sin(Φ)
* sin(θ)
r * cos(Φ)
r
représente encore le la rayon de la sphère. Cette équation
va nous permettre d'obtenir les coordonnées x,y,z de chaque point
de la sphère à une latitude et longitude données.
Pour une sphère Φ varie de 0° à 360° et θ
de -90° à +90°. Pour une demi sphère θ variera
uniquement de 0° à 90°.
Dans notre monde virtuel, on travaille toujours sur des donées
discrètes
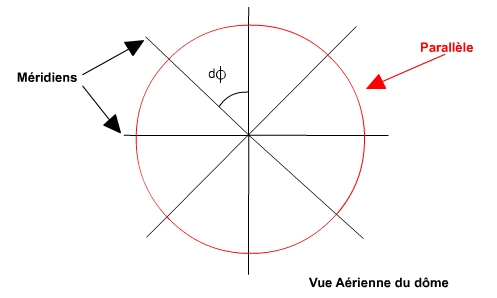
(ie non continue), la figure 1 en est un parfait exemple. On y distingue
trois type de lignes : les méridiens (les anneaux vericaux), les
parallèles (les anneaux horizontaux) et des diagonales. A partir
du nombre de méridiens et de parallèles on définit
une résolution.
Résolution
= nb méridiens X nb parallèles
Lorsque
la résolution tend vers l'infinie on passe du cas discret au cas
continue. Il n'est pas nécessaire d'avoir une résolution
supérieure à 500 pour avoir l'illusion de la continuité.
Voici l'algorithme
que nous allons utiliser :
Pour
ind_parallèle = 0 à nb_parallèle.
{
Pour ind_méridien
= 0 à nb_méridien.
{
dθ = ( ind_parallèle
/ nb_parallèle ) * ( Pi/2 )
dΦ = ( ind_méridien
/ nb_méridien ) * ( 2 Pi )
x = r * sin(dΦ) * cos(dθ)
z = r * sin(dΦ) * sin(dθ)
y = r * cos(dΦ)
}
}
Figure
2
to be continued...
|